Plane Drawings of Lobsters

In this post we show how to use Gephi to find a nice drawing of a graph with hundreds of vertices. A nice drawing in this context is one that has few edge crossings and whose nodes are regularly distributed over a fixed area with a small number of different edge lengths.

Ideally we would like to find a reproducible method for drawing graphs that is guaranteed to always produce a nice drawing in the above sense. The method demonstrated below does not entirely achieve this but is a useful first step in the right direction.

In future posts we hope to develop these methods by using scriptable tools and improved techniques to enhance the reproducibility of this method.

Lobster graphs

For simplicity here we consider only lobster graphs. From MathWorld:

a lobster is a tree having the property that the removal of leaves leaves a caterpillar

where

a caterpillar is a tree such that removal of its endpoints leaves a path graph.

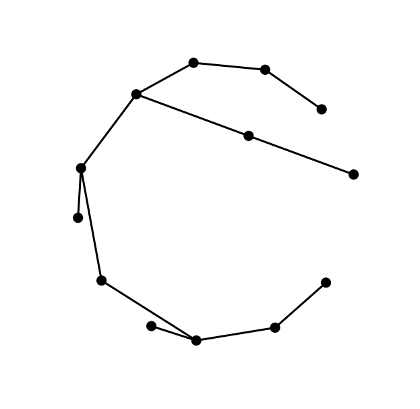
Lobsters, being trees, are planar graphs and with small lobsters plane drawings like the one above can be achieved easily. Notice that although this drawing is not an especially elegant one it does have the benefits of making both the planarity and the lobsterity of the graph clear.

For comparison, consider the following drawing of a large lobster graph.

This drawing (the random node placement layout Gephi defaults to on loading a new graph) reveals neither the planarity nor the lobsterity of the graph.

Incidentally, the above lobster graph has 287 vertices and, being a tree, 286 edges. It was generated in Python using NetworkX. The following command creates a graph file in GEXF format (Graph Exchange Format) which can be downloaded here.

$ python -c "import networkx as nx;nx.write_gexf(nx.random_lobster(100, 0.5, 0.5, seed=0), 'lobster.gexf')"

The random_lobster(n, p, q, seed=None) function returns a lobster with approximately n vertices in the backbone, backbone edges with probability p and leaves with probability q. The seed is set to zero for the sake of reproducibility.

Force-directed drawing algorithms

The type of drawing we are looking for, one with as few edge crossings and different edge lengths as possible is the kind of drawing aimed for by force-directed algorithms. Such methods use simulations of forces between nodes to decide node placements. Electrical forces have the effect of making non-adjacent nodes move further apart and spring forces between adjacent nodes have the effect of reducing the variety of edge lengths.

Gephi makes the standard Fruchterman-Reingold force-directed algorithm available alongside a layout method unique to Gephi called Force-Atlas.

These two layout methods, although both built on force-directed foundations, produce wildly different layouts with the same lobster graph input.

Beginning with random placement of nodes, the Fruchterman-Reingold algorithm implementation in Gephi produces a layout having uniform distribution of nodes across a disk; albeit one with very many edge-crossings.

This is a well-known problem with force-directed methods. The algorithm has probably discovered a local minimum. Unfortunately this local minimum is poor in comparison with the global minimum.

The Force-Atlas algorithm, on the other hand, creates a layout which has few crossings but without the nice node distribution of the Fruchterman-Reingold layout.

One of the great benefits of Gephi is that is easy to experiment with combining these methods to produce a layout which has the benefits of both.

Combining Force-Atlas with Fruchterman-Reingold

First using the Force-Atlas method to find a nearly plane drawing and then using the Fruchterman-Reingold algorithm on the resulting drawing produces a new drawing that is both nearly planar and has evenly distributed nodes with relatively few different edge lengths.

Another benefit of Gephi, not illustrated here, is that some of the layout methods allow for interaction during execution. This means that, where there are edge-crossings we can manually move vertices around a little bit to help eliminate them. So a layout like the one shown, which has few edge crossings can probably be improved to a plane drawing with a little manual interaction.

References

• Force-directed graph drawing on Wikipedia.